Любой компьютер по своей сути является высокотехнологичнымм калькулятором и ничем более.
Несколько лет назад вирусились ролики по Майнкрафту, в которых прямо в игре запускали калькуляторы, PacMan и даже Майнкрафт внутри Майнкрафта.
Со стороны это выглядит нереально. Игроки сделали виртуальные микросхемы внутри игры, и те работают прямо как настоящие процессоры. И всё это из простейших переключателей, похожих на настенные в каждом доме.
Из таких же состоят вычислительные ядра CPU в наших компьютерах, поэтому простые люди в Майнкрафте смогли повторить гениальные изобретения инженеров процессоров.
Ниже доступно объясняю, каким образом из этих элементарных переключателей под названием «транзистор» делают невероятно мощные чипы.
КРАТКО◦ Что такое транзистор, простейший выключатель в процессоре
◦ Как транзисторы превращаются в логические мини-блоки
◦ Как из простейших мини-блоков делают самостоятельные калькуляторы
◦ Как самостоятельные калькуляторы заставили работать друг с другом и исполнять код
◦ Как транзисторы научили считать обычные числа, а не двоичный код
◦ Из таких калькуляторов сделаны процессоры CPU
По какой логике фундаментально работает компьютер

Подробнее будем смотреть на самый верхний «слой» этого пирога – на железную составляющую программы
Начнём с понимания, по какому вообще принципу CPU работает на уровне своей архитектуры.
Возьмём простую аналогию.
Если бы компьютер был поваром, и ему дали задачу сделать торт, он бы разбил её не только по этапам приготовления, но и по этапам создания каждого компонента.
Логика там была бы такой:
1. Соединить элементарные частицы в нужные молекулы
2. Создать из молекул металлы, минералы и органику
3. Создать из металлов, минералов и органики печь, инструменты и ингредиенты
4. Замесить тесто, испечь коржи, сделать крем
5. Собрать торт.
Каждый новый этап поднимает уровень задачи на новый уровень абстракции. При этом каждый инструмент, который используется на новом этапе продолжает состоять из элементов из прошлого этапа.

Схема ядра CPU от Intel. Вычисления в процессоре происходят в маленьких блоках, самые известные это ALU, арифметико-логические блоки
В компьютере из маленьких вычислительных блоков собирается блок покрупнее, а из них собираются блоки ещё больше и так далее, пока всё это дело не будет выглядеть как программа с интерфейсом.
Только в случае компьютера он оперирует не молекулами (пока), а нулями и единицами.
Как любая молекула состоит из элементарных частиц (протон, электрон, нейтрон), так и нули и единицы формируются электронами, проходящими через транзисторы.
Ноль: на транзистор не подаётся ток
Единица: на транзистор подаётся ток.
Эта бинарная система используется для создания более сложных блоков. Далее разбираемся, как именно.
Что такое транзистор, простейший выключатель в процессоре
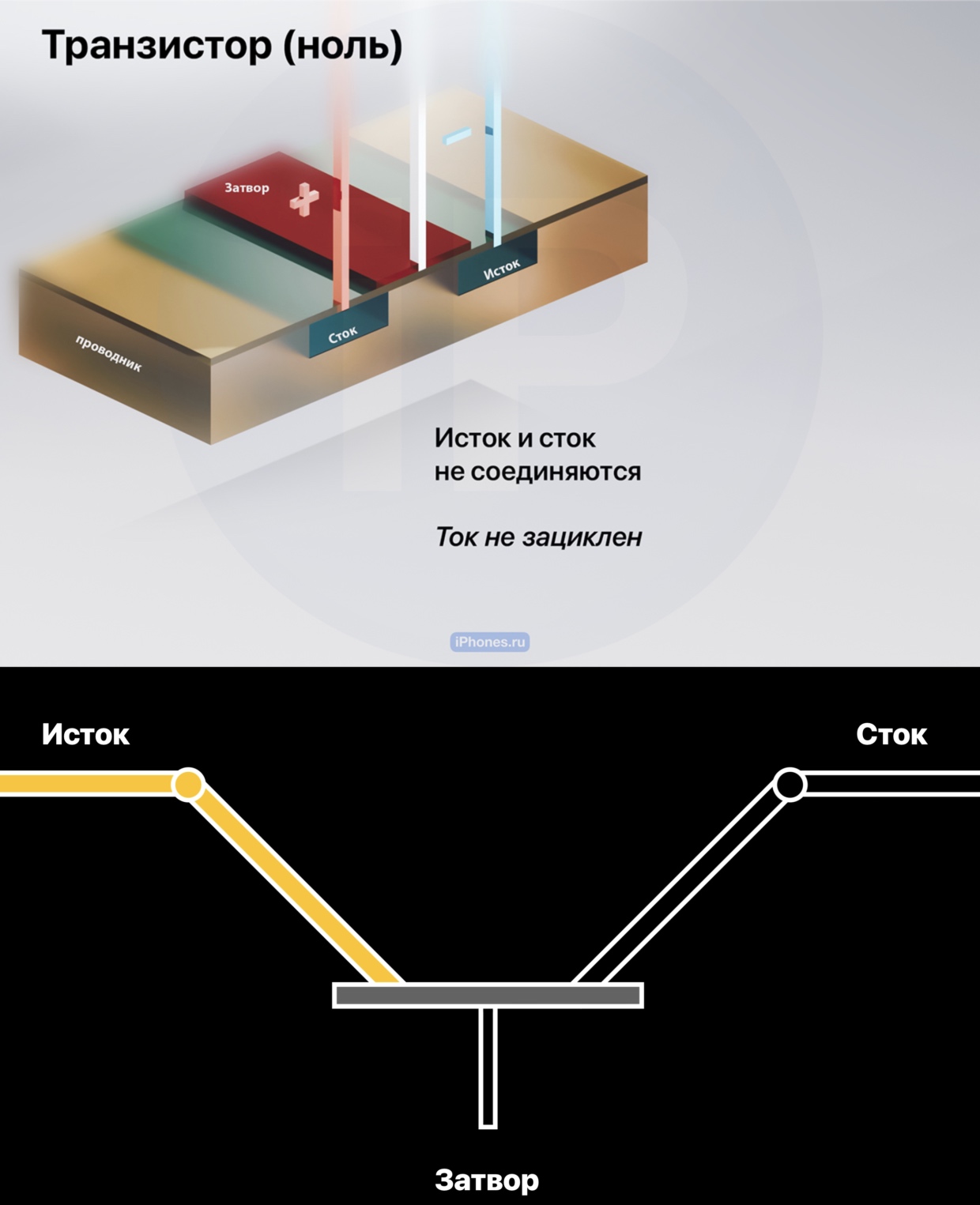
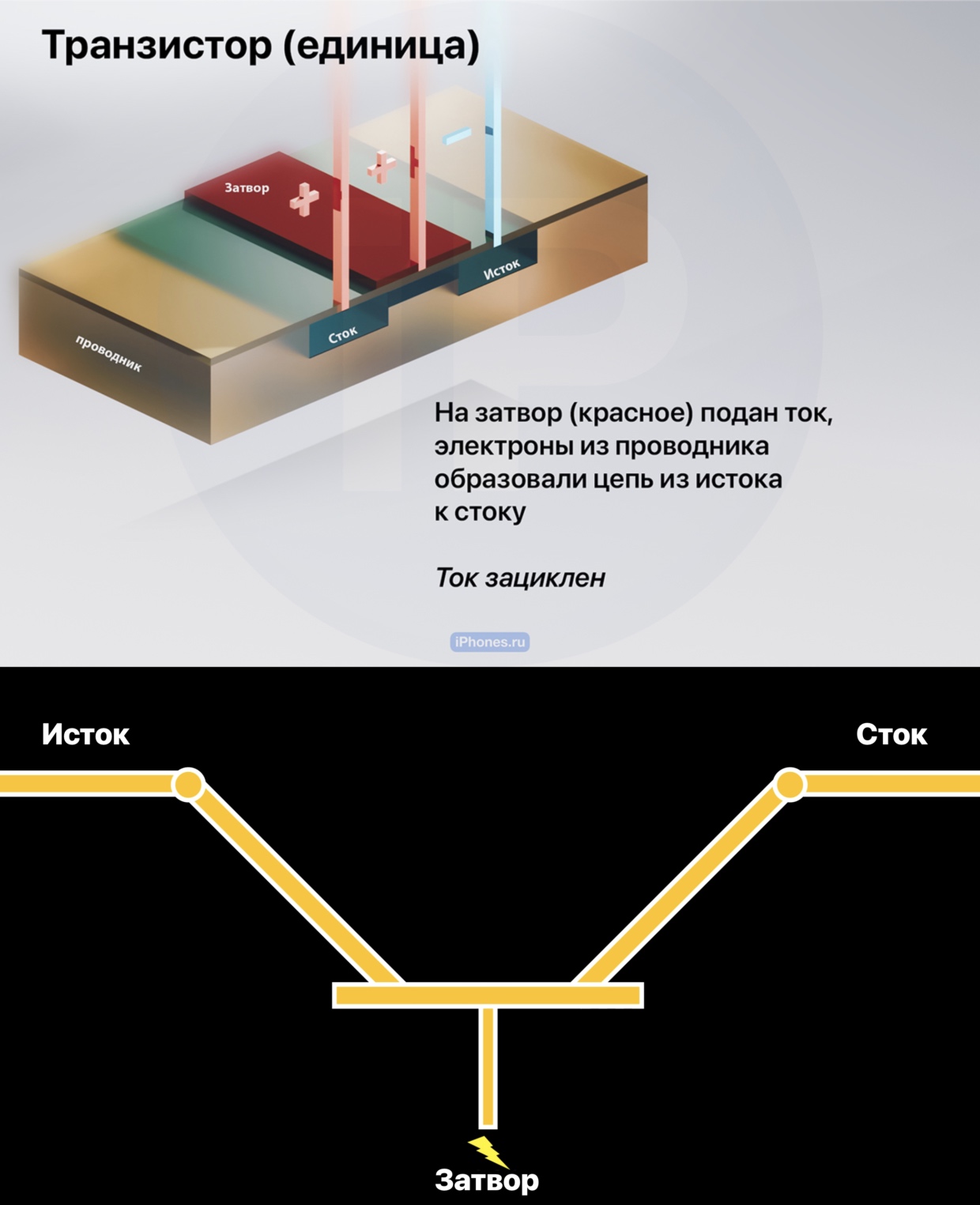
На картинки можно нажать, чтобы увеличить. Заряды плюса и минуса в полевых MOSFET-транзисторах, из которых состоят CPU, могут менять своё положение
Транзистор представляет собой маленький «блок» с тремя контактами: исток (вход), сток (выход) и затвор (управляющий).
У него только одна задача: блокировать ток (0) или пропускать его (1).
▪︎ В обычном состоянии вход и выход не соединяются в цепь, и транзистор находится в состоянии 0.
▪︎ Если подать небольшое напряжение на управляющий затвор, он превращается в проводник и открывает путь для движения электронов из истока в сток или из входа в выход. Так транзистор переходит в состояние 1.
Как только ток проходит через транзистор, вычисление уже происходит, поэтому процесс расчёта операций почти моментальный.
📰 В современных процессорах таких «переключателей» миллиарды, а операций триллионы в секунду, поскольку сами транзисторы размером с 20 атомов кремния.
Транзисторы бывают разных видов, принципа работы и составов. Так их производят.
Когда один транзистор соединяют с другим, появляется простейший вычислительный блок. Тут и начинается магия.
Как транзисторы превращаются в логические мини-блоки

Если соединить транзистор один за другим и закольцевать систему лампочкой на конце, для её включения нужно, чтобы оба транзистора «включились», то есть проводили ток
Допустим, с помощью транзисторов мы хотим включить лампочку при определённых условиях.
Например, чтобы она загоралась, только когда оба переключателя включены. Для этого нам нужно соединить их в нужной последовательности.
Если поставить один транзистор за другим, то потенциально мы можем получить четыре результата, потому что каждый транзистор может иметь по два значения (выключен и включён):
0+0=0
1+0=0
0+1=0
1+1=1
Такая простая цепочка формирует самый базовый вычислительный блок И (AND).
Он так называется, потому что для результата 1, то есть включения лампочки, нужно, чтобы первый транзистор и второй транзистор имели значение 1, то есть оба были проводниками электричества.
А теперь посмотрим, как сделать, чтобы лампочка загоралась, если хотя бы один переключатель включен – например, так делают в отеле, когда рубильник есть у кровати и входа в номер.

Если соединить транзисторы параллельно друг другу и подвести к ним лампочку, она загорится, даже если только один «рубильник» будет проводить электричество
Для этого нужно соединить транзисторы параллельно друг другу и объединить в одну цепь. Потенциальных исходов останется четыре, но с другим результатом:
0+0=0
1+0=1
0+1=1
1+1=1
Эта цепочка формирует базовый вычислительный блок ИЛИ (OR).
Название такое, потому для достижения 1 нужно, чтобы хотя бы один из двух транзисторов имел значение 1, то есть проводил ток.

Ещё есть третий базовый блок НЕ (NOT). Это обычный транзистор, который меняет своё состояние на противоположное через замыкание цепи до подключения транзистора.
Таким образом выключенный транзистор (0) не мешает току иди к лампочке, а включённый (1) прекратит его подачу и выключит свет.
Так мы пришли к первому уровню абстракции, когда мы уже смотрим не на транзисторы, а на базовые вычислительные блоки.

На схемах эти блоки имеют своё обозначение, чтобы не рисовать все транзисторы каждый раз и проще понимать цепочку
Но их не хватит, чтобы охватить все варианты с переключателями. А если нам нужно, чтобы 1+1 было равно 0?
❗️Если сложить 1+1, то получится 2. Однако в двоичной системе двойки нет.
Поэтому начинается новый десяток, который выглядит как 1 рядом с 0 – другими словами, просто 10. Такая закономерность называется целочисленным переполненением или Overflow output.
Простым словами это значит «ноль пишем, один в уме».
Значит, нужен такой блок, который в примере 1+1 даст 0, а единицу будет «держать в уме», как в примерах в столбиком.
Поэтому наши мини-блоки нужно объединить в блоки покрупнее.
Как из простейших мини-блоков делают самостоятельные калькуляторы

Этот блок нужен, чтобы писать «0» в десятках, когда складываем 1+1 в двоичной системе
Допустим, теперь мы хотим подключать не лампочку, а сделать одноразовый калькулятор двоичной системы.
Чтобы получить блок, который умеет из двух единиц делать ноль, нужно совместить несколько логических операций в одну.
Для этого берут навык транзистора инвертировать значение (блок НЕ, NOT) и параллельно совмещают с блоком И (AND). А в конце пропускают новые данные через блок ИЛИ (OR).
Как это происходит:
1. Единицы проходят сразу через два блока: НЕ и И.
2. Инвестирующий блок превращает их в 0 и тем самым одновременно блокируют блокам И возможность превратить их в единицы
3. Получившиеся два значения 0 поступают на блок ИЛИ, которые выдаёт конечное значение 0.

Здесь ясно видно, почему результат при складывание двух единиц получается нулевым
👉 Единицы нельзя просто пропустить через инверторы, потому что в таком случае при попытке сложить 0 и 0, те превратятся в две единицы и блок ИЛИ превратит их в 1 вместо необходимого 0. Поэтому добавляется блок И.
Зато в схеме, где НЕ и И идут параллельно, а потом попускают значение через ИЛИ, результат получается правильным: оба исходных значения 0 инвертируются, но взаимоисключают друг друга при проходе через блок И, которому нужно, чтобы оба значения были единицами.
Такая особая схема имеет своё название XOR.
Если перейти на следующий уровень абстракции, и в одном блоке совместить XOR и И, то мы получим микросхему, которая умеет корректно складывать 1+1 и получать тем самым значение 10 с целочисленным переполнением (ноль пишем, один в уме). Такой блок называется Half Adder, полусумматор.
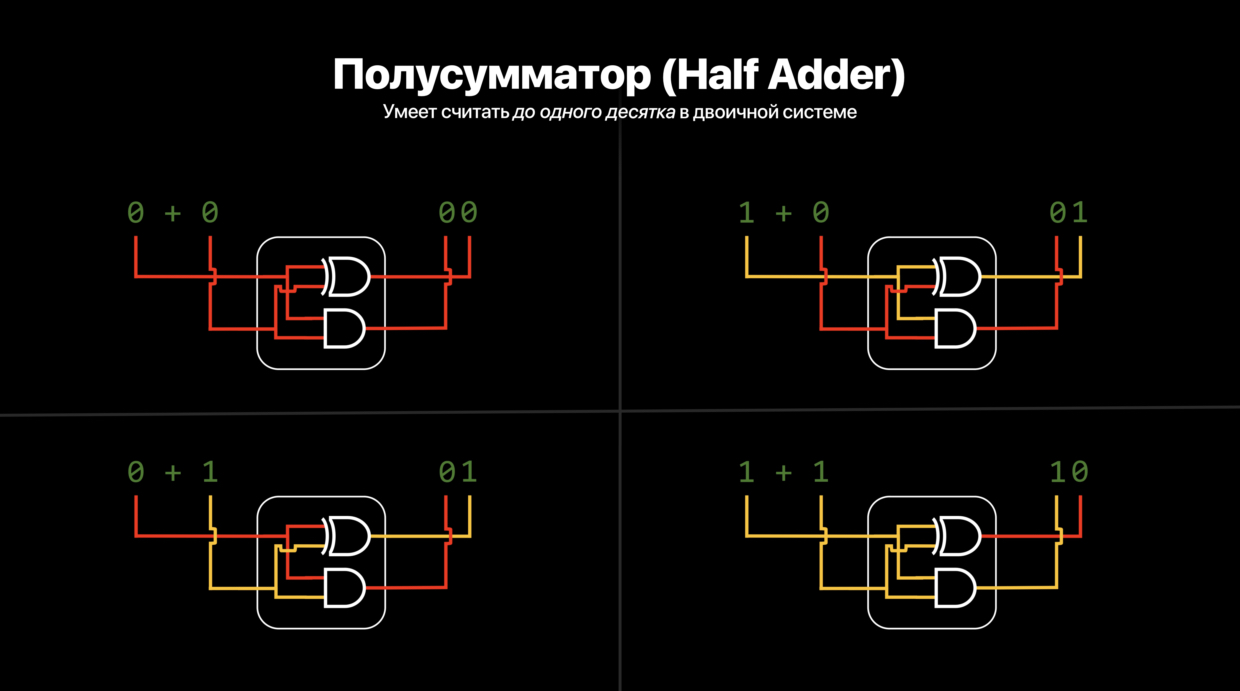
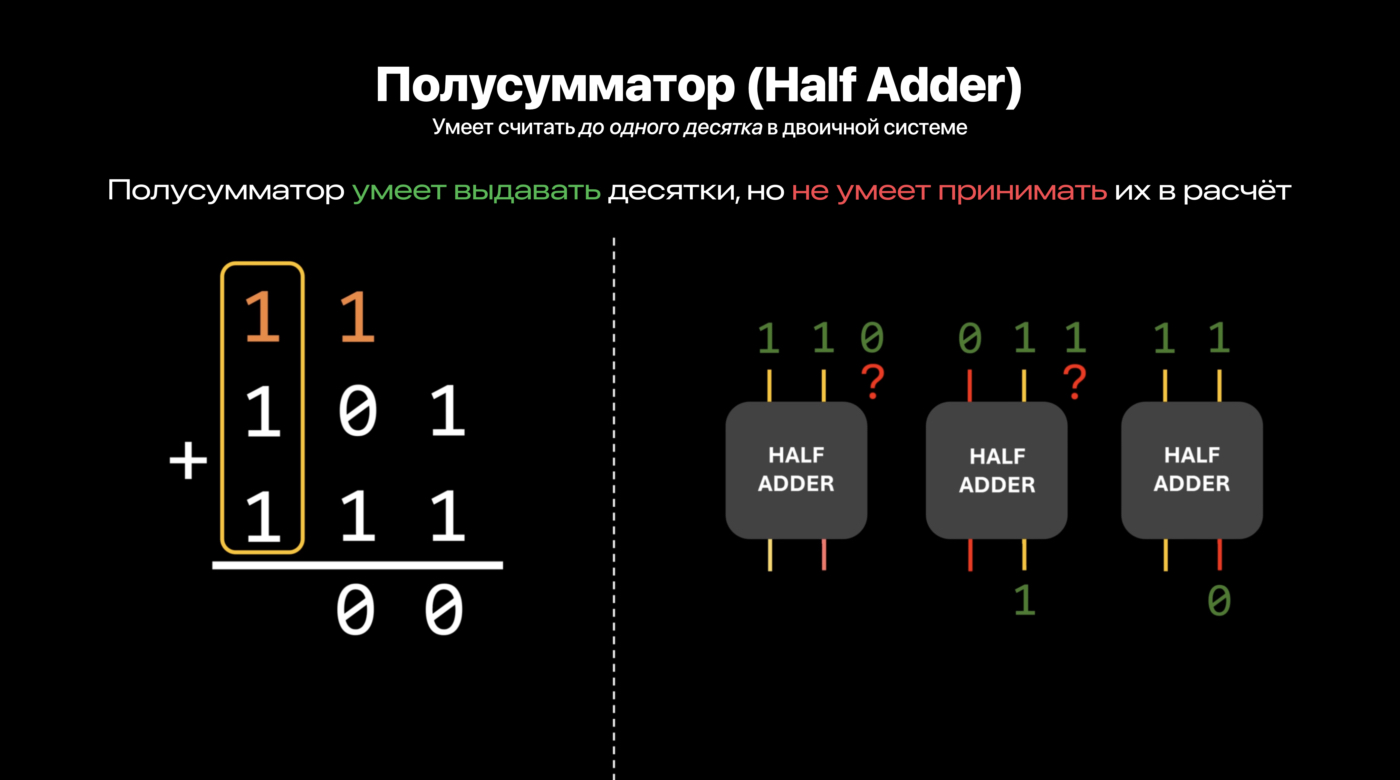
При этом мини-блоки XOR и И решают задачу из двух чисел параллельно и независимо друг от друга: первый вычисляет значения «единиц», а второй значения «десятков» двоичной системы.
🧮 Пример работы полусумматора.
Как происходит вычисление 1+1=10
Блок XOR: 1+1=0
Блок И: 1+1=1.В итоге получается код 10.
Полусумматор берёт два значения и выдаёт два новых значения.
Но чтобы продвинуться дальше, нужен следующий уровень абстракции: для связанных друг с другом расчётов нам нужно, чтобы результаты первого вычисления были исходными данными для обработки во второй раз.
Как самостоятельные калькуляторы заставили работать друг с другом и исполнять код
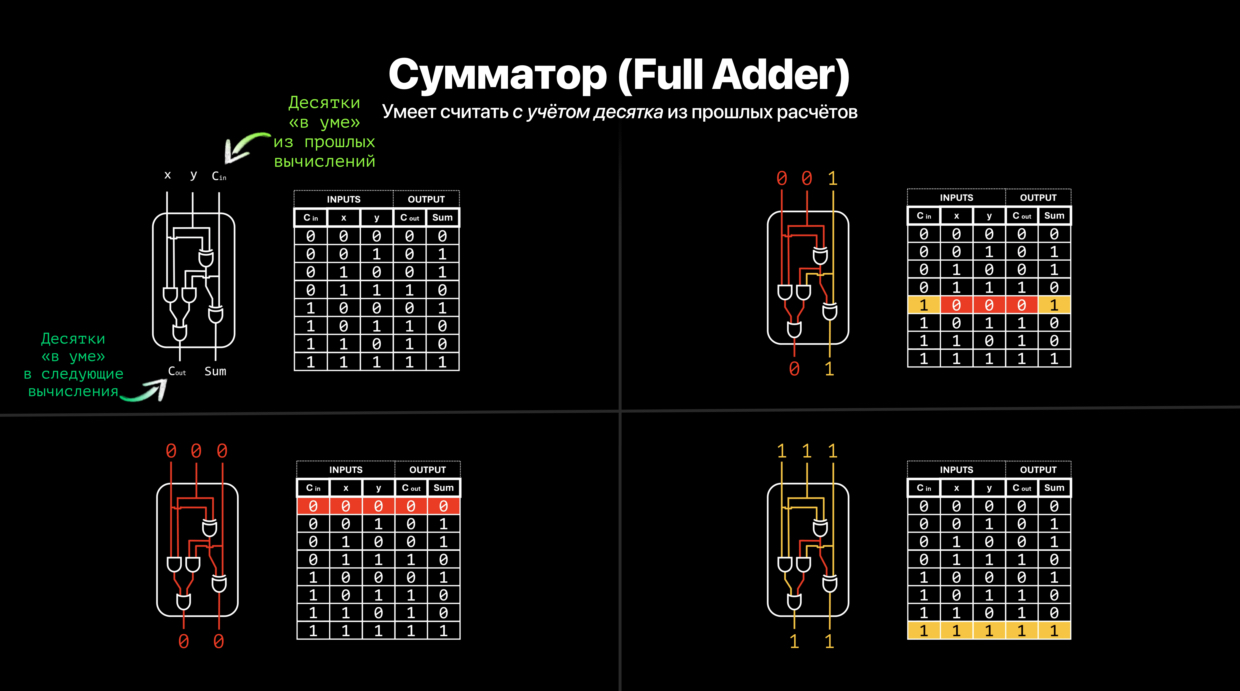
Наконец, чтобы сделать полноценный калькулятор двоичной системы, который будет понимать, откуда и какие значения брать, новый блок должен брать два исходных значения и третью единицу или ноль, которые «держит в уме» из предыдущего расчёта.
Для этого полусумматор модифицировали для возможности брать сразу три значения: на выходе он всё так же имеет блоки XOR и И, однако к ним подведены два блока И и ещё один XOR.
Они помогают корректно направить единицы и нули, чтобы из трёх значений получалось два: значение единиц и значение десятков.
Так получается новый блок Full Adder, сумматор.
Пример работы сумматора.
Нам нужно сложить 11 и 11. В десятичной системе это 3+3.
Сначала сумматор складывает «однёрки» на конце. Получается 10. 0 пишется в конец, один в уме.
Далее он складывает первые числа 1 и 1 и добавляет к ним 1, которую «держит в уме» их прошлого расчёта. Получается 10+1=11.
Теперь 11 вписывается перед 0. Получается 110.
По бинарной системе смотрим, что двоичный код 110 равен 6 в десятеричной системе, то есть всё верно.

В этом примере складывается 101 и 111, в десятеричной системе это 5+7. В итоге получается 1100 в двоичной системе и 12 в десятеричной
Если не объединить полусумматоры для учёта целочисленного переполнения (умения держать один в уме), калькулятор моментально сделает ошибки и будет непригодным к использованию.
🚀💥 Реальная катастрофа, потому что не держали «один в уме».
В 1996 году разбилась американская ракета Intelsat 708 со спутником на борту сразу после запуска с китайского космодрома.
Расследование выявило ошибку в схеме транзисторов во CPU встроенного компьютера, которая привела к неверным расчётам траектории во время полёта. Это привело к отклонению и падению.
Однако сами по себе сумматоры не умеют ставить выходные числа одно за другим, чтобы получился код десятичной системы.
Для этого их объединяют в 8-битовые кластеры, которые адаптированы под интерпретацию компьютером в понятные нам числа.
Как транзисторы научили считать обычные числа, а не двоичный код

Сумматоры, которые умеют «переносить» остаток на следующий сумматор, теперь можно объединить в настоящий калькулятор.
Обычные числа кодируются 8-битовым двоичным кодом благодаря переносу остатков.
Для этого восемь сумматоров (Full Adder) объединяют в один блок, который теперь умеет считать привычные нам числа.
Внутри него каждый сумматор (Full Adder) отвечает за расчёт только своей ячейки и цельночисленного переполнения в последовательности кода.
Перевод двоичного кода в десятеричный выглядит так.
◆ 0 из привычной нам десятеричной системы обозначается как 0000 0000.
◆ 1 обозначается как 0000 0001.
◆ 2, как мы выяснили, в двоичном коде обозначается как 0000 0010.
Тут мы видим, как перенесли остаток на один уровень вперёд. Продолжим.
◆ 3=1+2, то есть нам нужно сложить 0000 0001 и 0000 0010. Получается 0000 0011.
И тут начинается самое интересное.
◆ 4=1+3 или 0000 0001 плюс 0000 0011. Последнее число будет 0, предпоследнее тоже, поскольку происходит перенос остатка первого числа. И мы снова держим 1 в уме. Значит, третим с конца числом будет 1. Получается 0000 0100.
◆ И так доходим до 255, которое в двоичном коде выглядит как 1111 1111.
Блок, который отвечает за вычисление этого кода из восьми цифр называется 8-bit Full Adder, 8-битовый сумматор.
Он всегда получает 8 цифр исходных данных и выдаёт 9 цифр, из которых восемь цифр результата плюс одна цифра цельночисленного переполнения (один в уме).
👉 Чтобы получить
256, первый 8-битовый сумматор сообщает подключённому к нему соседнему 8-битовому сумматору, что у него есть 1 в уме. И тот, беря его во внимание, превращает код числа из 8-битового в 16-битовый:
256=1+255, то есть0000 0001плюс 1111 1111.Суммирование новой единицы с единицей на конце превращает её в «0 с одним в уме», что вызывает цепную реакцию для всех остальных единиц в восьмибитовой строчки, поэтому и нужно добавлять второй сумматор для пропитывания числа в новом формате.
В итоге вычисления дают нам
0000 0001 0000 0000.А механически это выглядит как два 8-битовых сумматора с восемью сумматорами внутри каждого.
И тут мы, наконец, подходим к тому, как устроена самая базовая единица ядра в процессоре, арифметико-логический блок ALU.
Из таких калькуляторов сделаны процессоры CPU. А в GPU и нейроядрах есть и другие
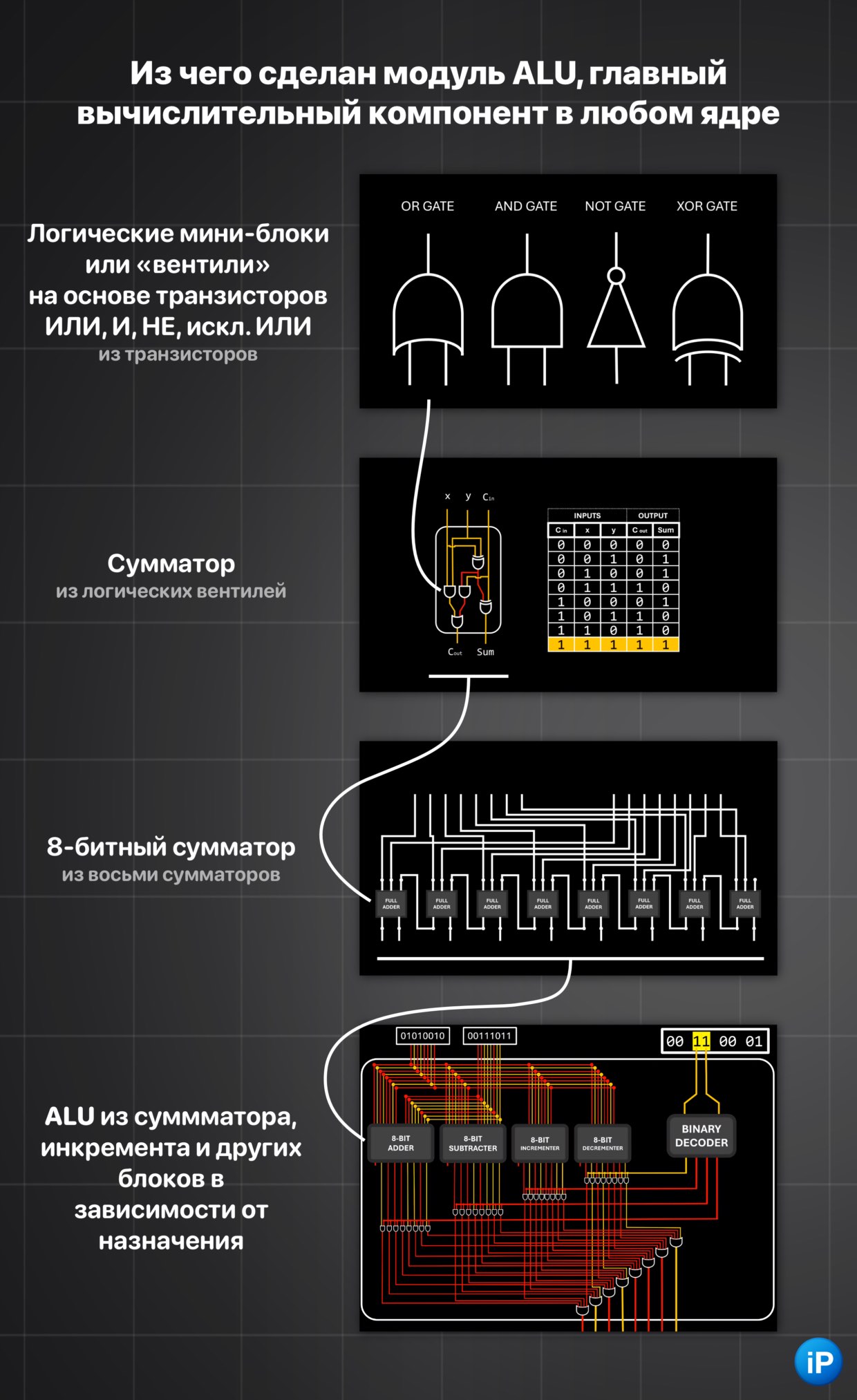
По рассмотренному нами выше принципу увеличения уровней абстракции создают микросхемы, которые умеют отнимать любой число, отнимать только единицу и добавлять только единицу к поступающим числам.
Они образуют собой арифметико-логический блок ALU, который выполняет операции вычислений на базовом уровне.
Эти операции далее по более сложным каналам трансформируются в:
• Слова на экране
• Изменения в масштабе фотографий
• Декодирование видеопотока
• Положение мыши
• Загруженные из интернета страницы
• Перемещение файлов из одного места в другое
• И много других процессов вашей ОС.
В ядрах GPU и NPU кроме арифметико-логических блоков ALU со сложением и вычитанием есть ещё векторные и тензорные блоки, состоящие из модулей для вычисления матриц и умножений.
Они отвечают за:
• Эффективную тренировку и работу нейросетей
• Просчёт геометрии
• Отрисовку текстур в играх
• Трассировку лучей
• И другие задачи, завязанные на параллельных вычислениях.
Теперь вы знаете, из каких мельчайших строительных блоков состоят наши процессоры.
На самом деле, кроме ALU, элементов в CPU гораздо больше, но большинство остальных занимается управлением данными и их правильным декодированием в зависимости от задачи – это уже «менеджеры», а не рядовые рабочие, которыми являются блоки из этого поста.
На более высоких уровнях абстракции находятся уже ядра, но не всегда. Например, в SSD всё на ячейках транзисторов и заканчивается. На эти темы у нас набралось уже много статей.
В тему
◆ Чем отличается процессор CPU от GPU. Разбираемся, почему в одном восемь ядер, а в другом тысячи
◆ Это казалось невозможным. Как в крохотные чипы SSD сейчас помещается целых 8 ТБ памяти





 (18 голосов, общий рейтинг: 4.89 из 5)
(18 голосов, общий рейтинг: 4.89 из 5)












9 комментариев
Форум →